暑假的时候圣上跟我说到 N 狗追戏问题，描述大概是这样：

在一个圆上坐着 N 只狗，它们恰好均分圆周，从某一时刻开始它们同时朝逆时针方向最近的狗进行移动，且任意时刻所有的狗速率相等。问狗狗的行动轨迹。

回去自己想了一下，既然所有的狗的行为是一样的，那么在任意时刻，它们必定还是在一个圆心不变的圆上，并且这个圆的半径是随时间逐渐减小的。 这样大脑里就浮现出一个旋转并且逐渐变小的圆。初步就把这个曲线 “想象” 出来了，其具有一种自相似的性质，放大部分跟整体相同（分形）。

“它们同时朝逆时针方向最近的狗进行移动” 也就是说任意时刻狗狗的速度总是指向下一只狗，换句话说就是轨迹曲线上每点的切线斜率总是与那两只狗当时所在位置确定的直线相同。 这种几何特性用极坐标分析的话要简单的多（如图，以 N = 3 为例）。

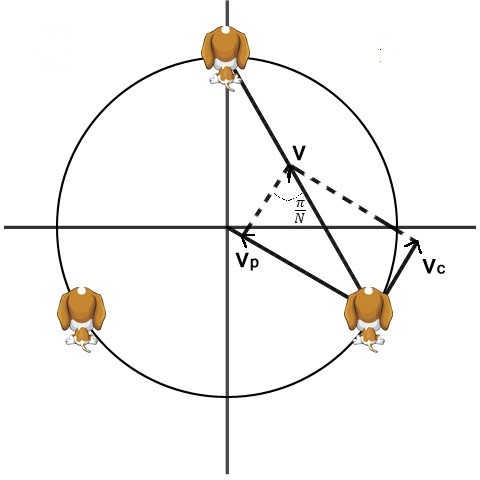
于是有分速度 $V_{\rho}$（指向圆心）和 $V_c$（与圆相切）保持如下关系：

\[\frac{V_{\rho}}{V_c}=\tan{\frac{\pi}{N}}\]

于是有微元关系：

\[\frac{\mathrm{d}r}{r\tan(\mathrm{d}\theta)}=\frac{\mathrm{d}r}{r\mathrm{d}\theta}=-\tan{\frac{\pi}{N}}\]

添加负号是因为当 θ 增大时，r 却是减小的。

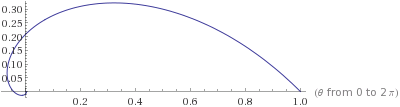
到此，微分方程一出，轨迹就很好解出来了。 使用 Wolfram Alpha 解得是个对数螺线。

形状大概是这样（由 Wolfram Alpha 生成）：

最近修改于 2010-02-16 02:16