22. 投票箱 The Ballot Box
In an election, two candidates, Albert and Benjamin, have in a ballot box $a$ and $b$ votes respectively, $a \geqslant b$, for example, 3 and 2. If ballots are randomly drawn and tallied, what is the chance that at least once after the first tally the candidates have the same number of tallies?
在一次选举中,两位候选人 A、B 分别在投票箱中有 $a$ 张和 $b$ 张选票并且 $a\geqslant b$。假如唱票是每次随机取出(这里应该是看作取出一张)并且计数,那么在唱票途中至少有一次两人得票相等(平局)的概率是多少?
思 考 的 空 间
由于 $a>b$,那么以 B 开始的唱票序列中间必然会至少出现一次平局。 每个以 B 打头的平局序列都有一个对应的以A开头的平局序列(比如 BAAB 与 ABBA,BABA 与 ABAB,BBAA 与 AABB)。 因此所求概率即为两倍唱票序列以 B 开始的概率: \(\dfrac{2b}{a+b}\)
另一个相关问题:贝特朗投票问题(Bertrand's Ballot Problem)则是问 “唱票途中 A 一直领先 B 的概率是多少?”,由 W. A. Whitworth 在 1878 年提出并给出结果,其考虑的事件恰好是上题所求事件的补集,Howard Grossman 在 1946 年给出了一个图形解释:
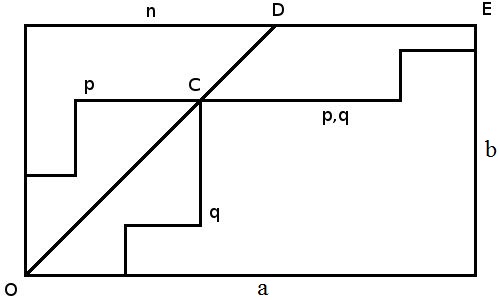
从 O(0,0) 开始,整个唱票过程可以看成在如上图坐标系中的离散游走。向右移动一个单位即本次唱票为 A,向上移动一单位则为 B,目标是要到达 E 点 (a,b)。
- OD 这条对角线则表示所有的平局情况,可以看出倘若第一步向上一个单位(即第一张选票为 B ),唱票路径必然穿过 OD,即出现平局。
- 以 OD 为轴,存在一条与上述平局路径相对应的路径,其以对称路径到达同一平局点之后以相同路径抵达终点E。如图中的 p 路径与 q 路径。
此两点均与之前论述相吻合。
倘若 A 的唱票数一直领先 B(即 A 的个数均大于 B 的个数),唱票路径必须在 OD 的右下方且不能有交点,显然为所有未出现平局的情况。因此答案为
\[1-\dfrac{2b}{a+b}=\dfrac{a-b}{a+b}\]
参考
- The Ballot Box Problem
- Howard D. Grossman. Fun with lattice-points. Duke Mathematical Journal, 14:305–313, 1950.
23. 猜币游戏中的平局 Ties in Matching Pennies
Players A and B match pennies $N$ times. They keep a tally of their gains and losses. After the first toss, what is the chance that at no time during the game will they be even?
思 考 的 空 间
A 在 $N$ 次游戏中赢 $m$ 轮的概率为 $\displaystyle{\binom{N}{m}/2^N}$
根据 22 题的结果,若 A 在 $N=2n$ 次游戏中赢 $m$ 轮,则
$m<n$,出现平局的概率为 $\dfrac{2m}{N}$
$m\geqslant n$,出现平局的概率为 $\dfrac{2(N-m)}{N}$
于是总的平局概率为 \(P(tie)=\displaystyle{\dfrac{1}{2^{N-1}}\left(\sum^{n-1}_{m=0}\dfrac{m}{N}\binom{N}{m}+\sum^{N}_{m=n}\dfrac{N-m}{N}\binom{N}{m}\right)}\)
又
\[\begin{aligned} &\displaystyle{\dfrac{m}{N}\binom{N}{m}}=\dfrac{m}{N}\times\dfrac{N!}{m!(N-M)!}=\dfrac{(N-1)!}{(m-1)!(N-m)!}\displaystyle{=\binom{N-1}{m-1}} \\ &\displaystyle{\dfrac{N-m}{N}\binom{N}{m}}=\dfrac{N-m}{N}\times\dfrac{N!}{m!(N-M)!}=\dfrac{(N-1)!}{m!(N-m-1)!}\displaystyle{=\binom{N-1}{m}} \end{aligned}\]
那么总的平局概率可写为
\[P(tie)=\displaystyle{\dfrac{1}{2^{N-1}}\left(\sum^{n-2}_{m=0}\binom{N-1}{m}+\sum^{N-1}_{m=n}\dfrac{N-m}{N}\binom{N-1}{m}\right)}\]
根据二项式定理有
\[\begin{aligned} P(tie)&=\displaystyle{\dfrac{1}{2^{N-1}}\left(\sum^{N-1}_{m=0}\binom{N-1}{m}-\binom{N-1}{n-1}\right)} \\ &=\displaystyle{\dfrac{1}{2^{N-1}}\left(2^{N-1}-\binom{N-1}{n}\right)} \\ &=\displaystyle{1-\binom{N-1}{n}/2^{N-1}} \end{aligned}\]
易得没出现平局的概率为
\[\begin{aligned} \displaystyle{\binom{N-1}{n}/2^{N-1}}&=\dfrac{(N-1)!}{n!(n-1)!}\times\dfrac{1}{2^{N-1}} \\ &=\dfrac{N\times(N-1)!}{n!(n-1)!\times2n}\times\dfrac{1}{2^{N-1}} \\ &=\dfrac{N!}{n!n!}\dfrac{1}{2^N} \\ &=\binom{N}{n}/2^N \end{aligned}\]
同理易得 $N=2n+1$ 的情况为
\[\displaystyle{\binom{N-1}{n}/2^{N-1}}\]
补充问题
Suppose A and B are candidates for office and there are $2n$ voters, $n$ voting for A and $n$ for B. In how many ways can the ballots be counted so that B is never ahead of ?
这个问题的答案是卡特兰数(Catalan Number),解答可参考 《TAOCP》 Vol.1 的 Answers To Excercises Section 2.2.1
The following elegant solution uses a "reflection principle" due to D. André (1887): There are obviously $\binom{2n}{n}$ sequences of S's and X's that contain $n$ of each. It remains to evaluate the number of inadmissible sequences (those that contain the right number of S's and X's but violate the other condition). In any inadmissible sequence, locate the first X for which the X's outnumber the S's. Then in the partial sequence leading up to and including this X, replace each X by S and each S by X. The result is a sequence with $(n+1)$ S's and $(n - 1)$ X's. Conversely for every sequence of the latter type we can reverse the process and find the inadmissible sequence of the former type that leads to it. For example, the sequence XXSXSSSXXSSS must have come from SSXSXXXXXSSS. This correspondence shows that the number of inadmissible sequences is $\binom{2n}{n-1}$. Hence $a_n=\binom{2n}{n}-\binom{2n}{n-1}$.
《计算机程序设计艺术(第1卷)》(苏运霖[译]) 的译文如下
下面的精彩解法使用由 D.André 给出的 “反射” 原理:显然有 $\binom{2n}{n}$ 个含 S 和 X 各 $n$ 个的序列。剩下的是计算不允许的序列数(它包含正确个数的 S 和 X,但是违背其他条件)。在任何不允许的序列中,定出使得 X 的个数超过 S 的个数的第一个X的位置。然后,在导致并包括这个 X 的部分序列中,以 S 代替所有的 X 并以 X 代替所有的 S。结果是一个有 $(n+1)$ 个 S 和 $(n-1)$ 个 X 的序列。反过来,对于后一种类型的每个序列,我们都能逆转这个过程,而且找出导致它的前一种类型的不允许序列。例如,序列 XXSXSSSXXSSS 必然来自 SSXSXXXXXSSS。这个对应说明,不允许序列的个数是 $\binom{2n}{n-1}$。因此 $a_n=\binom{2n}{n}-\binom{2n}{n-1}$。[Comptes Rendus Acad. Sci. 105 (Paris, 1887), 436~437]
同理,若 22 题是问 “唱票途中A一直不落后B的概率是多少?”,则其答案为
$\displaystyle{\frac{1}{\binom{a+b}{b}} \left[ \binom{a+b}{b}-\binom{a+b}{b-1} \right] =\frac{a+1-b}{a+1}}$
变种问题
12 个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
有编号为 1 到 n (n 可以很大,不妨在这里假定可以达到 10 亿)的若干个格子,从左到右排列。 在某些格子中有一个棋子,不妨设第 xi 格有棋子 (1⩽i⩽k,1⩽k⩽n)(1⩽i⩽k,1⩽k⩽n) 每次一个人可以把一个棋子往左移若干步,但是不能跨越其它棋子,也要保证每个格子至多只有一个棋子。 两个人轮流移动,移动不了的为输,问先手是不是有必胜策略。
16 个人按顺序去买烧饼,其中 8 个人每人身上只有一张 5 块钱,另外 8 个人每人身上只有一张 10 块钱。烧饼 5 块一个,开始时烧饼店老板身上没有钱。16 个顾客互相不通气,每人只买一个。问这 16 个人共有多少种排列方法能避免找不开钱的情况出现。
给定 n 个数,有多少种出栈序列?
饭后,姐姐洗碗,妹妹把姐姐洗过的碗一个一个地放进碗橱摞成一摞。一共有 n 个不同的碗,洗前也是摞成一摞的,也许因为小妹贪玩而使碗拿进碗橱不及时,姐姐则把洗过的碗摞在旁边,问:小妹摞起的碗有多少种可能的方式?
一个有 n 个 1 和 n 个 -1 组成的字串,且前 k 个数的和均不小于 0,那这种字串的总数为多少?
n 个节点构成的二叉树,共有多少种情形?
n 对括号有多少种匹配方式?
圆桌周围有 2n 个人,他们两两握手,但没有交叉的方案数
在图书馆一共 6 个人在排队,3 个还《面试宝典》一书,3个在借《面试宝典》一书,图书馆此时没有了《面试宝典》了,求他们排队的总数?
一位大城市的律师在他住所以北 n 个街区和以东 n 个街区处工作,每天她走 2n 个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
最近修改于 2013-05-29 15:02