偏差-方差分解 Bias-Variance Decomposition

设希望估计的真实函数为

\[f=f(X)\]

但是观察值会带上噪声，通常认为其均值为 $0$

\[Y=f(X)+\epsilon, E\left[\epsilon\right]=0\]

假如现在观测到一组用来训练的数据

\[D=\left\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),...,(\mathbf{x}_N,y_N)\right\}\]

那么通过训练集估计出的函数为

\[\hat{f}=\hat{f}(X;D)\]

为简洁起见，以下均使用 $\hat{f}(X)$代替$\hat{f}(X;D)$

那么训练的目标是使损失函数的期望最小（期望能表明模型的泛化能力），通常损失函数使用均方误差 MSE (Mean Squred Error)

\[\begin{aligned} E\left[Loss(Y,\hat{f})\right]&=E\left[MSE\right] \\ &=E\left[\frac{1}{N}\sum^N_{i=1}(y_i-\hat{f}(\mathbf{x}_i))^2\right] \\ &=\frac{1}{N}\sum^N_{i=1}E\left[ (y_i-\hat{f}(\mathbf{x}_i))^2\right] \end{aligned}\]

注意: $y_i$ 和 $\hat{f}$ 都是不确定的; $\hat{f}$ 依赖于训练集 $D$, $y_i$ 依赖于 $\mathbf{x}_i$.

下面单独来看求和式里的通项 $\begin{aligned} E\left[\left(y_i-\hat{f}(\mathbf{x}_i)\right)^2\right]&=E\left[\left(y_i\color{red}{-f(\mathbf{x}_i)+f(\mathbf{x}_i)}-\hat{f}(\mathbf{x}_i)\right)^2\right] \\ &=E\left[\left(y_i-f(\mathbf{x}_i)\right)^2\right]+E\left[\left(f(\mathbf{x}_i)-\hat{f}(\mathbf{x}_i)\right)^2 \right]+2E\left[\left(y_i-f(\mathbf{x}_i)\right)\left(f(\mathbf{x}_i)-\hat{f}(\mathbf{x}_i)\right)\right] \\ &=E\left[\epsilon^2\right]+E\left[\left(f(\mathbf{x}_i)-\hat{f}(\mathbf{x}_i)\right)^2 \right]+2\left(E\left[y_if(\mathbf{x}_i)\right]-E\left[f^2(\mathbf{x}_i)\right]-E\left[y_i\hat{f}(\mathbf{x}_i)\right]+E\left[f(\mathbf{x}_i)\hat{f}(\mathbf{x}_i)\right]\right) \\ &=Var\left\{noise\right\}+E\left[\left(f(\mathbf{x}_i)-\hat{f}(\mathbf{x}_i)\right)^2\right] \end{aligned}$

$E\left[y_i f(\mathbf{x}_i)\right]=f^2(\mathbf{x}_i)$ 因为 $f$ 和 $\mathbf{x}_i$ 是确定的而 $E\left[y_i \right]=f(\mathbf{x}_i)$

$E\left[f^2(\mathbf{x}_i)\right]=f^2(\mathbf{x}_i)$ 因为 $f$ 和 $\mathbf{x}_i$ 是确定的

\[E\left[y_i \hat{f}(\mathbf{x}_i)\right]=E\left[\left(f(\mathbf{x}_i)+\epsilon\right)\hat{f}(\mathbf{x}_i)\right]=E\left[f(\mathbf{x}_i)\hat{f}(\mathbf{x}_i)+\epsilon\hat{f}(\mathbf{x}_i)\right]=E\left[f(\mathbf{x}_i)\hat{f}(\mathbf{x}_i)\right]\]

$E\left[\epsilon\hat{f}(\mathbf{x}_i)\right]=0$ 因为测试集中的噪声 $\epsilon$ 独立于回归函数的预测 $\hat{f}(\mathbf{x}_i)$

$E\left[\epsilon^2\right]=Var\left\{noise\right\}$ 噪声方差

\[\begin{aligned} E\left[\left(f(\mathbf{x}_i)-\hat{f}(\mathbf{x}_i)\right)^2\right]&=E\left[\left(f(\mathbf{x}_i)\color{red}{-E\left[\hat{f}(\mathbf{x}_i)\right]+E\left[\hat{f}(\mathbf{x}_i)\right]}-\hat{f}(\mathbf{x}_i)\right)^2\right] \\ &=E\left[\left(f(\mathbf{x}_i)-E\left[\hat{f}(\mathbf{x}_i)\right]\right)^2\right]+E\left[\left(E\left[\hat{f}(\mathbf{x}_i)\right]-\hat{f}(\mathbf{x}_i)\right)^2\right]+2E\left[\left(f(\mathbf{x}_i)-E\left[\hat{f}(\mathbf{x}_i)\right]\right)\left(E\left[\hat{f}(\mathbf{x}_i)\right]-\hat{f}(\mathbf{x}_i)\right)\right] \\ &=E\left[\left(f(\mathbf{x}_i)-E\left[\hat{f}(\mathbf{x}_i)\right]\right)^2\right]+E\left[\left(E\left[\hat{f}(\mathbf{x}_i)\right]-\hat{f}(\mathbf{x}_i)\right)^2\right]+2\left(E\left[f(\mathbf{x}_i)E\left[\hat{f}(\mathbf{x}_i)\right]\right]-E\left[E\left[\hat{f}(\mathbf{x}_i)\right]^2\right]-E\left[f(\mathbf{x}_i)\hat{f}(\mathbf{x}_i)\right]+E\left[E\left[\hat{f}(\mathbf{x}_i)\right]\hat{f}(\mathbf{x}_i)\right]\right) \\ &=bias^2\left\{\hat{f}(\mathbf{x}_i)\right\}+variance\left\{\hat{f}(\mathbf{x}_i)\right\} \end{aligned}\]

$E\left[f(\mathbf{x}_i)E\left[\hat{f}(\mathbf{x}_i)\right]\right]=f(\mathbf{x}_i)E\left[\hat{f}(\mathbf{x}_i)\right]$ 因为 $f$ 是确定的

$E\left[E\left[\hat{f}(\mathbf{x}_i)\right]^2\right]=E\left[\hat{f}(\mathbf{x}_i)\right]^2$ 　

$E\left[f(\mathbf{x}_i)\hat{f}(\mathbf{x}_i)\right]=f(\mathbf{x}_i)E\left[\hat{f}(\mathbf{x}_i)\right]$ 因为 $f$ 是确定的

$E\left[E\left[\hat{f}(\mathbf{x}_i)\right]\hat{f}(\mathbf{x}_i)\right]=E\left[\hat{f}(\mathbf{x}_i)\right]^2$

$E\left[\left(f(\mathbf{x}_i)-E\left[\hat{f}(\mathbf{x}_i)\right]\right)^2\right]=bias^2\left\{\hat{f}(\mathbf{x}_i)\right\}$ 偏差

$E\left[\left(E\left[\hat{f}(\mathbf{x}_i)\right]-\hat{f}(\mathbf{x}_i)\right)^2\right]=variance\left\{\hat{f}(\mathbf{x}_i)\right\}$ 方差

最终

$$E\left[\left(y_i-\hat{f}(\mathbf{x}_i)\right)^2\right]=Var\left\{noise\right\}+bias^2\left\{\hat{f}(\mathbf{x}_i)\right\}+variance\left\{\hat{f}(\mathbf{x}_i)\right\}$$

因此，要使损失函数的期望 $E\left[Loss(Y,\hat{f})\right]$ 最小，既可以降低 bias，也可以减少 variance。这也是为什么有偏的算法在一定条件下比无偏的算法更好。

　　　　　　　　偏差（bias）描述的是算法依靠自身能力进行预测的平均准确程度

　　　　　　　　方差（variance）则度量了算法在不同数据集上表现出来的差异程度

下面来自《The Elements of Statistical Learning》 P38 Figure 2.11 的图则阐释了模型复杂度与偏差、方差、误差之间的关系：

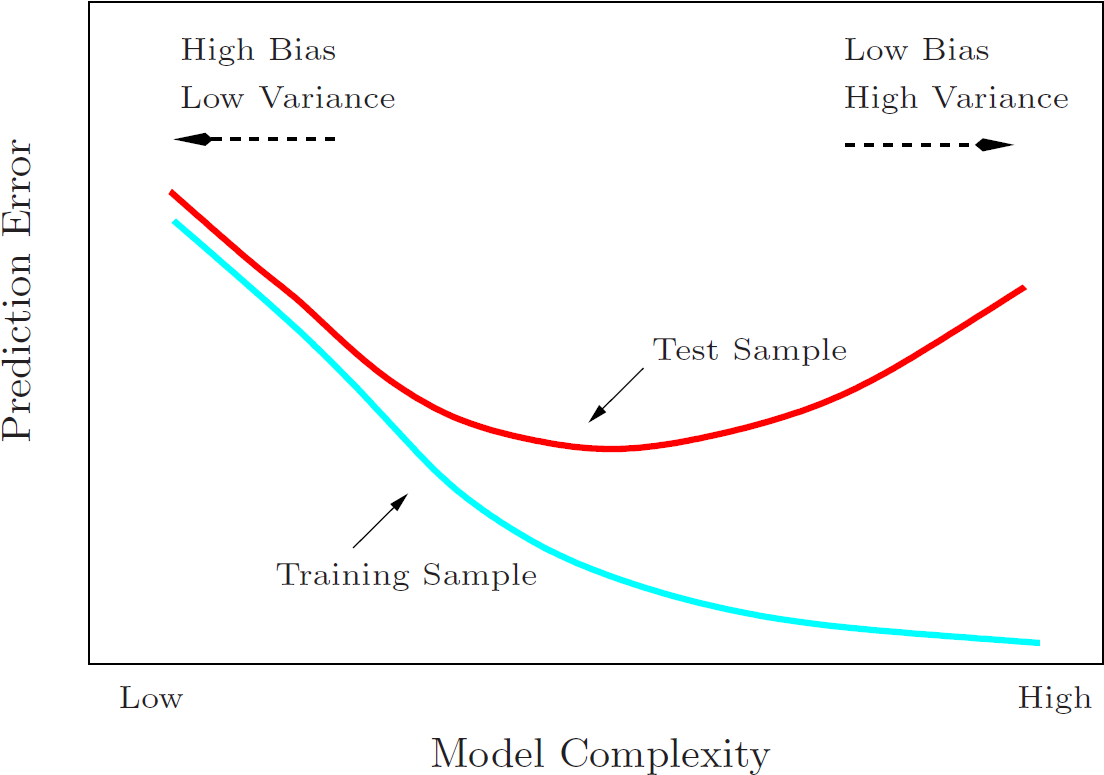
《The Elements of Statistical Learning》 Figure 2.11

PS:

装袋算法 Bagging 通过 bootstrap 对训练集重采样来并行训练多个分类器（均匀采样），主要是降低方差 variance。

提升算法 Boosting 通过迭代调整样本权重来串行组合加权分类器（根据错误率采样），因而主要是降低偏差 bias（同时也减少方差 variance）。

参考:

最近修改于 2013-05-14 22:40