无穷大和传销、赌博、股市、次贷危机
传销模式盈利秘诀不在于商品,而在于金字塔式的分级分层发展会员的提成规则。传销组织也即 “老鼠会”。 考虑一个纯粹的 “老鼠会”,仅有三条规则:
- 发展会员。
- 向上一级缴纳会费。
- 发展会员时向下一级收缴会费,50% 自留,50% 交给上一级。
易得任何一级会员,只要发展两个下级会员便可保本,发展第三个便开始赚钱。 最佳情况是,所有会员都能赚钱,而且级别越高,入会越早,会费越高,赚钱也会越多,然而唯一的附加条件是,入会人数无穷大。然而由于入会人数不可能达到无穷大,在 “老鼠会” 最末级的会员们就是最终的资金输出者,他们肯定赔钱。
再来考虑赌博的博弈问题,这里按 1 : x,x 大于 1 的赔率计算,怎样保证赌博稳赚不赔?很简单,采用赌注加倍的战术。 如果第一次输了,第二次就将赌注加倍,就算前 N 次输了,只要第 N+1 次赢了,你就赚钱。这个博弈战术理论上是没有什么缺陷的,然而必要的前提是,赌资无穷大。 而在国外合法的赌场上,每一盘的赌资都设定了上限,不允许 “赌资加倍” 策略的出现,否则因为资本远大于比赌场老板的赌徒的赌资可看成无穷大,这样将实现稳赚不赔。
一年前,中国的股民都在窃喜股市的疯涨,原因很简单,只要有资金往股市涌,股市就涨,不断涌入就会不断涨高。 于是,只要进入股市,人人都能赚钱,然而那个讨厌的前提条件阴魂不散:涌入股市的资金一天一天增多,趋于无穷大。 在上证指数从 1700 涨到 6300 时,很少有股民关心企业的真正价值,他们只是乐观地相信明天会有更多的人,更多的资金涌入股市,可惜这种信念不现实,不可能有无穷大的资金涌入股市。 于是我们看到,许多外资在中国全民皆股时撤离股市后,中国一片惨绿。
拥有超前观念的经济学家热衷提倡提前消费,没现金买房没关系,银行先借你,这叫 “按揭”。 连首付都拿不出来,也没关系,再搞个新金融产品,叫 “次贷”。这样一来,大大提高了消费,刺激了市场,房地产开发商会建更多的房,政府也会收获更多的 GDP。 接下来会有下一的房价上涨,市场一片繁荣。可惜前提条件又来了:房价年年涨,银行资本无穷大。 当然,这是不可能的,当消费信心丧失,次贷危机来临时,我们才明白,银行乃至整个国家的资本都不是无穷大的,经济发展的规模和速度是受到有限的资本约束的,过度不科学的提前消费必将受到惩罚。
随机算法和围棋AI
倘若要求如下正方形内不规则图形的面积是多少,也许微积分可行,但也相当复杂。
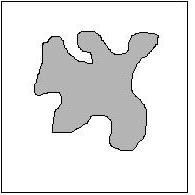
波兰数学家乌拉姆天才地提出了另一种方法,用一个正方形将该不规则图形围住,然后用计算机仿真,模拟随机地向正方形内掷飞镖。 当掷出的次数足够大,从统计的角度来说,落入正方形内的飞镖数和落入该不规则图形内的飞镖数之比应等于这两个图形面积的比值(正方形的面积当然很容易求)。 这真是个聪明的方法,他把我们平常的计算过程逆转过来了,通常我们是已知其他物理量求概率,而这里是利用概率反过来去求物理量。 这种随机仿真的概率方法后来以世界著名赌城 “蒙特卡罗” 命名。
Tips: 下面是常见的概率算法及特点
| 算法 | 是否有解 | 解特点 |
|---|---|---|
| Monte Carlo 算法 | 一定能求出一个解 | 解不一定正确,时间越长,解正确的概率越大 |
| Las Vegas 算法 | 不一定能求出一个解 | 解一定正确 |
| Sherwood 算法 | 一定能求出一个解 | 解一定正确 |
最近一次围棋大赛中,MOGO 程序获得了冠军,原因就在于,它将通常的策略树搜索算法(UCT)和蒙特卡罗算法(MC)结合起来了。 因为落子点的策略树搜索(把所有可能的下子顺序都拿出来考虑)随着深度的增加对时空的要求成级数增长,因此在达到十分有限的深度时就得停止,这样便不能很好地对落子点进行评估。 于是蒙特卡罗算法在这时开始帮忙,其思想是假设你这步棋已经下到这了,找两个傻子,让他们随便下,把棋下完,看看是黑棋胜还是白棋胜。 只有两个傻子,这结局太有偶然性了,那么我们找 10000 对傻子来下 10000 盘棋,然后统计一下是黑棋赢的多还是白棋赢的多,这样就得到了这一手棋的获胜概率, 然后我把所有可能下法的获胜概率都这样算出来,我们就能得出一个趋势,也即一个取胜概率,就能评估落子点的好坏选择获胜概率最大的下法。 这种随机算法虽然感觉有些碰运气,但事实上,目前看来还是十分有效(而且日后和专家系统结合的话将更加有效)。由于这个算法结合的策略,MOGO 目前在 19×19 的棋盘上也是非常强大的。
《决胜21点》中的一个概率问题
该题目原是美国《检阅》杂志的 “玛丽莲” 专栏上介绍的一道游戏性质的数学题,在美国引起了轰动,大约有 1000 所大中小学,从二年级的小学生到研究生都卷入了求解这个题目的讨论。 有趣的是,在给该专栏主持人玛丽莲小姐的 10000 多封来信中,有约 1000 封是具有博士头衔的读者写的,他们说,玛丽莲小姐的答案是错的。 玛丽莲小姐的题目是这样的:
有三扇可供选择的门,其中一扇后面是辆汽车,另两扇的后面都是一头山羊。 你当然想选中汽车。主持人先让你随意挑选。 比如你选了 1 号门,这时主持人打开的是后面有羊的一扇门(比如它是 3 号门),现在主持人问你:“为了有较大的机会选中汽车,你是坚持你原来的选择、还是愿意换选另一扇门?”
玛丽莲小姐公布的答案是:“应该换选另一扇门。”──这是说:她给你看 3 号门后面是羊之后,你原来选 1 号门的,应换选为 2 号门;你原来选 2 号门的,应换选 1 号门。 通常的想法是,主持人既然把没有车的那扇门打开了,剩下的两扇门后面是车是羊的可能性各占一半,坚持原来的选择也好,换选也好,选中车的机会都是二分之一。 博士们就是这样想的,你认为究竟谁对呢?
解:
这个问题的关键在于一个条件或者说一个暗示,即主持人知道门后面有什么并且希望游戏继续进行, 这样造成的一个推理结果是主持人打开一扇后面是羊的门的过程是主动有意的(简述为 “主持人选羊” 的原则)。 然而这个条件题目并没有明确地给出,而是间接地用语义和常识进行了暗示,不过这其实并不影响最后的综合考虑结果。
(a.1) 若主持人知道门后面有什么,那么他的选择不是随机的,实际上他很可能会是有意识的选择了后面有羊的门,而将有车的门留下。因此 3 号门就将有车的概率给了 2 号门,此时 2 号门的有车的概率为 2/3 了。
(b.1) 若主持人不知道门后面有什么,那么他打开一扇门跟你打开一扇门是一样随机的。这样的话剩下的两扇门概率相同,各为 1/2,因此换不换是一样的。
呵呵,会不会有些想不清楚了?没关系,接下来给出详细分析及计算:
易得,各个门里有车的概率均为 1/3 。
设 “主持人在 2 号门和 3 号门内选择一个门打开之后是羊并且车在剩下的那个门内” 为事件 A。
(a.2) 首先我们将 2 号门和 3 号门看作一个整体(概率均等时才能平滑捆绑),称作 2.5 号门。那么车在 2.5 号门的概率就是 1/3 + 1/3 = 2/3 。若车在 2.5 号门( P = 2/3 ), 主持人选择一个后面是羊的门的概率是 1,这时车在剩下的那个门内的概率也是 1;若车在 1 号门( P = 1/3 ), 主持人选择一个后面是羊的门的概率是 1,车在剩下那个门内的概率为 0。
得:P(A) = 2/3 × 1 × 1 + 1/3 × 1 × 0 = 2/3 (a.2.1)
这时 1 号门有车的概率小于另一个门,我们应改变选择。
(b.2) 若车在 2.5号 门( P = 2/3 ),主持人由于是随机选的,他选中羊的概率是 1/2 ,此时车在剩下的那个门内的概率为 1;若车在 1 号门,主持人怎么选都是羊,车在剩下的门内的概率为 0;
得:P(A) = 2/3 × 1/2 × 1 + 1/3 × 1 × 0 = 1/3 (b.2.1)
这时 1 号门有车的概率等于另一个门,改不改变无所谓。
比较 (a.2.1) 和 (b.2.1) 发现,差别就在于主持人选门的过程。若为 a 情况,我们有一个重要的信息:主持人总是肯定能选到羊并且优先选到羊,这个过程并不随机,或者说主持人选择一个门打开之后是羊概率总为 1。 而在 b 情况中,主持人选有羊的门是随机的,即可能打开一扇有车的门,这时游戏就没法继续玩了,所以和 a 相比,b 有 1/3 的概率流失,即游戏无法继续的概率,而对于 a 情况, 主持人总会选羊(“主持人选羊” 原则),游戏肯定能继续进行,因此那 1/3 的概率就加在了剩下的那个门上。
事实上,在实际情况中我们也只能猜测主持人的信息和动机。也许他不知道门后面有什么,也许他的想法很简单,随便打开一个门,若里面是车,对不起,你 Game Over 了。 但要是里面是羊,他就想增加游戏的刺激性和趣味性让你再选一次,这时改不改变选择是一样的,但是从心理角度来分析的话,改变选择若是没得到车,后悔程度将更大,因此人们害怕改变选择; 也许主持人知道后面有什么,为什么我们推出 “主持人选羊“ 原则?因为主持人既然知道门后面有什么,他是会想增加游戏的刺激性和趣味性的, 即努力让游戏多进行会,否则若是车不在 1 号门内,他会马上把有车的门打开,然后一脸抱歉的说,噢,非常遗憾。这是不太符合题目条件的。 但是这个常识上的假设并不一定成立,因为主持人若是知道门后面有什么,他是可以自由控制选中有羊的门的概率的。 比如假设他知道 2 号门内有羊,3 号门内有车,但他并不直接作选择,而是自己做两个纸条一个写 2 一个写 3 抓阄,这时主持人选羊又回到了随机过程,概率为 1/2 ; 他也可以做三个纸条,两个上面写 2,另一个写 3,这时再抓阄的概率就是 2/3 了,他也可以两个写 3,另一个写 2,这时概率就只有 1/3 了;
所以接下来我们来推广地讨论一下这个问题:
设主持人知道门后面有什么的概率为 p,主持人选择的门后面是羊的概率为 t(只有在主持人知道信息时才能为 0-1 的任意一有理数,否则为 1/2 )。
则剩下的门内有车的概率与1号门内有车的概率之差为
[(1-p) × 1/3 + p × 2/3 × t] - 1/3
= (p/3)(2t-1)
可得当 t > 1/2 时应该改变选择,t ≤ 1/2 时不应该改变选择。
所以最终选择与主持人是否知道信息无直接关系,有直接关系的是 t,只是在我们熟知的实际生活中,若主持人知道门后有什么,这个 t 通常为 1。
有人说为了有更大的机会选中羊,就选择 1 号门不变,对吗?
参考:
《“无穷大”与“老鼠会”》,焦杜,《程序员》2008年12月
《围棋AI之路》,oyd
最近修改于 2008-12-17 12:28